Previously I have talked mostly about decision support systems, and sub-phenotypes of patients- groups of patients defined by their biomarkers, and how the identification of these groups is key to assessing what therapy will be successful. Today we will talk about a more fundamental problem which the computation of epicardial potentials based on the measurement of body surface potentials. In other words: How do we calculate the electrical activity on the heart surface, given voltage measurements on the patients torso? This is referred to as the inverse problem of electrocardiology, which is depicted in the figure to the right.
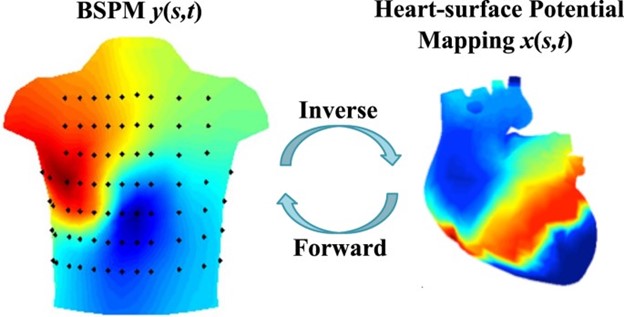
One of the more common approaches is the use of a transfer matrix, which performs the mapping from a 3D torso model to a 3D atria model. Such a mapping can be expressed with the following equation.
Where PA are the potentials in the atria, T is the transfer matrix, and PT are the measured torso potentials. Computing this transfer matrix is not as easy as the formula may suggest. The problem is ill-posed, and finding a stable solution is complicated. Different regularization methods are employed to find a solution that is stable and gives the desired results. At the end of the day, however, no matter how sophisticated the regularization, and how accurate the resulting transfer matrix, there will be a limiting factor that is inherent to the transfer matrix: Each atrial potential in PA (so each potential in a given place in the atria) can only be a linear combination of the torso potentials in PT. Realistically, the relationship is most likely more complicated, and we need a mathematical model that can capture these more complex relationships.
The question that we need to answer are to model this relationship is what the underlying physical phenomena are that constitute this relationship. Or do we? In one of my previous blog posts we talked about knowledge driven, and data driven reasoning. We can either use existing knowledge to model relationships, or we can throw lots of data at a model and optimize the model such that it captures these relationships. I would love to tell you more, but the competition may be lurking in these blog posts to steal ideas, so let me get a head start on this, and share the progress in the next blog post. Until then, stay safe!
Last but not least, do not forget to follow the progress of the ESR students involved and the project by checking all the official sites. See you soon.
[1] Yao, B., Yang, H. Physics-driven Spatiotemporal Regularization for High-dimensional Predictive Modeling: A Novel Approach to Solve the Inverse ECG Problem. Sci Rep 6, 39012 (2016).
Alex
Input your search keywords and press Enter.