Menu

Using Computer Models to Study the Heart

II. The Electrical Analogue

Patricia Martínez Díaz 

1. February.2021

Welcome back!

In our last post we explained that modeling is the process of using mathematical equations to describe the behavior of a system or a signal. Scientists use models to study the complex interactions between ions, channels, and intracellular mechanisms (tiny structures within the cell) that determine the electrical properties of a cell. Today you will learn about:

-The action potential

-What is an electrical analogue?

-The Nernst potential and Ohm´s Law

1. Look at the World from the top of a Mountain

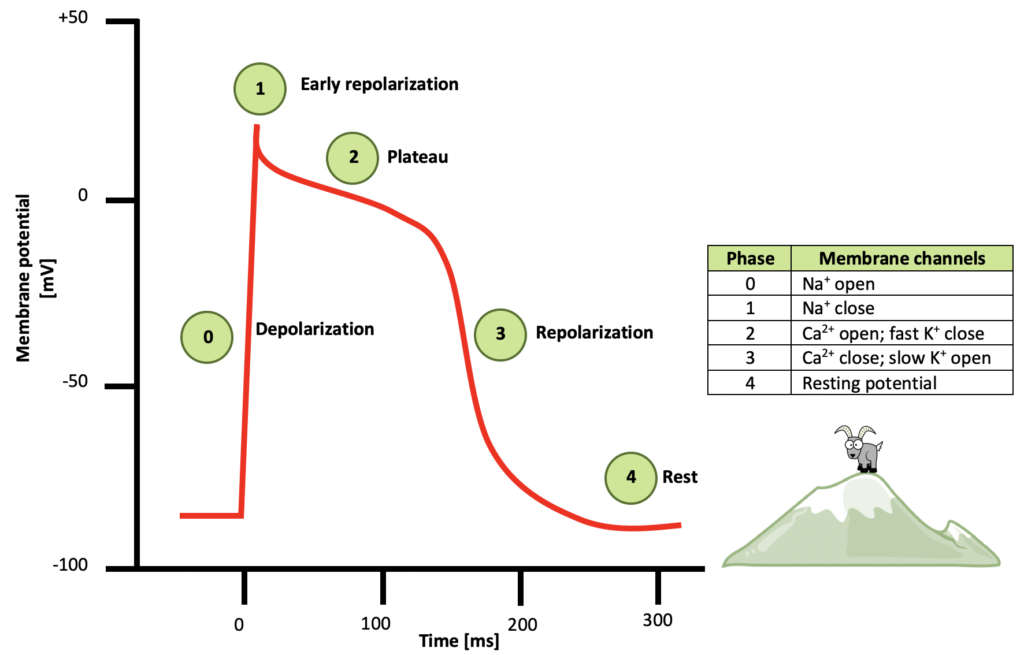
The action potential (AP) is a curve (with the shape of a mountain) that shows the changes in voltage of the cell membrane with respect to time. If you look at the following Figure 1, at rest the cell had an initial negative voltage. The movements of ions such as Potassium (K+) and Sodium (Na+) and make the cell reach a positive value. This process is called depolarization because the cell loses its negative pole. In a second stage, the AP shows a plateau, mainly caused by calcium ions (Ca2+) entering the cell. Finally, the cell comes back to its original resting state and becomes negative again, this is called repolarization. 

Figure 1. Action potential phases of a cardiac myocyte. Adapted from 2007 Pearson Education, Inc publishing as Benjamin Cummings

2. Magical forces and the Nernst Potential

But wait… why do ions move from one side of the cell to the other? It seems as if there are some “magical forces” that push ions and tell them where to go. Since we don’t use magic in science to explain the phenomena we observe, we will have to introduce two very important concepts: the electrochemical driving forces and the Nerst potential.

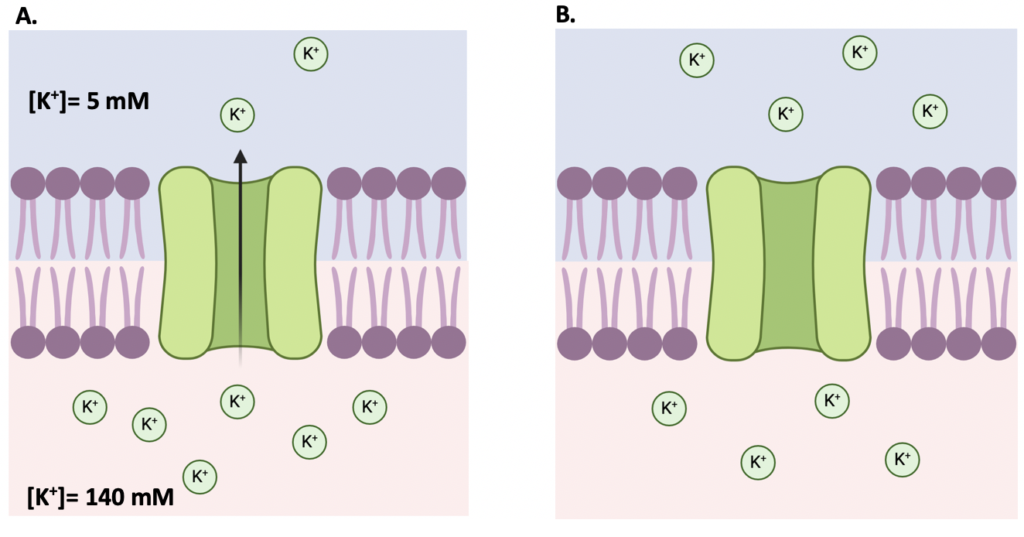
These magical forces are referred to as the electrical force, which considers the charge across the membrane, and the chemical force, which considers the number of ions across the membrane. At rest, most ionic channels are closed and do not allow the movement of ions. The concentration difference, or chemical force, inside and outside the cell causes ions to move from one side to the other. For example, when the cell is still at rest, the K+ concentration is higher inside the cell than outside of it, as seen in Figure 2A. When K+ channels are open, K+ ions will move out of the cell in order to reach an equilibrium, as depicted in Figure 2B. The rule is always like this: ions move from the compartment with the highest concentration to the one with the lowest concentration. In this case, as the cell is losing positive ions, the membrane potential will become negative. When the chemical gradient as well as the electrical charge are equal, it is said that the ion has reached equilibrium. The voltage at which an ion does not move across the membrane is called the Nernst potential.

Figure 2. The Potassium (K+) concentration gradient. A) Note that there is a higher K+ concentration (140 mM) inside the cell than outside of it (5 mM). B) The concentration of K+ is the same inside and outside the cell

3. The Electrical Analogue and Ohm´s Law

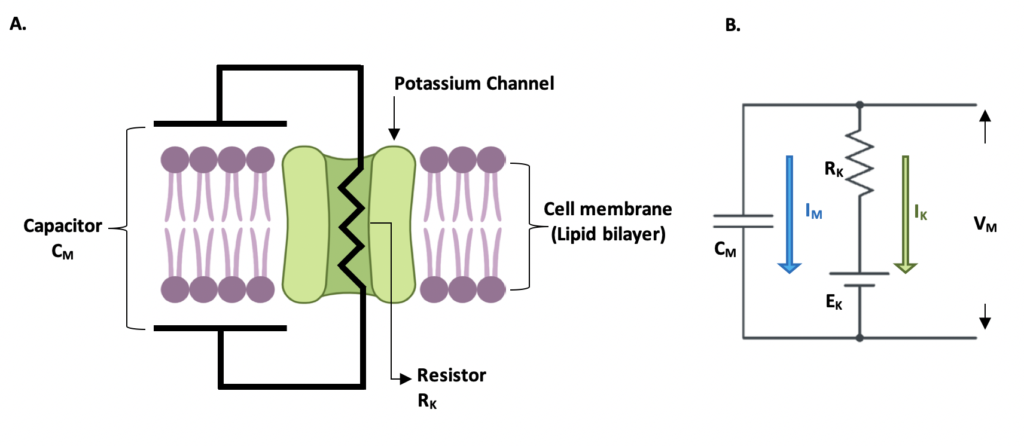
Finally, we will talk about the electrical analogue of the cell membrane. To study the electrical function of cells, scientists make their life easier by using an electrical circuit. It is important to recall that in general terms, the state of an electrical cell is determined by the movement of ionic currents through the membrane and the permeability of ionic channels. Permeability is a fancy word for stating whether a channel will allow (or block) the entrance of ions into the cell. This electrical circuit has three components: a resistor that represents the resistance of the ionic channels, a capacitor showing the ability of the membrane to store electrical charge, and batteries that represent the Nernst potential of each ion.  The electrical analogue is shown in the following image.

Figure 3. Electrical analogue of the cell membrane. A)The lipid bilayer is represented by a capacitor and the resistor represents the permeability of the ionic channel B) The electrical representation of the cell membrane CM: capacitance of the cell membrane, IM: current through the capacitor, RK resistance of the Potassium channel, EK: Ernst potential of the Potassium channel = -89.7 mV, VM: membrane potential, IK: Potassium current. Adapted from (1)

The capacitance of the cell membrane CM is defined by the following equation. Where q is the charge and VM is the membrane potential.

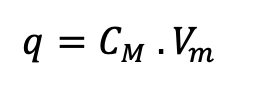
We can calculate the current (i) from the previous formula, since the current is the change of charge with respect to time (derivative):

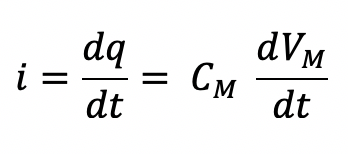
In the example of the Potassium channel, we could use Ohm’s law to calculate the ionic current IK. This law states that the amount of current (I) in a circuit depends on the voltage (V) and the resistance (R). Additionally, as we already know the equilibrium membrane voltage when there is no K+ movement (Yes! The Nernst Potential) instead of using the R, we could use another term: the conductance (G), which is nothing more than the inverse of R. The V in our equation is the difference between the membrane potential VM and the Nernst Potential EK.

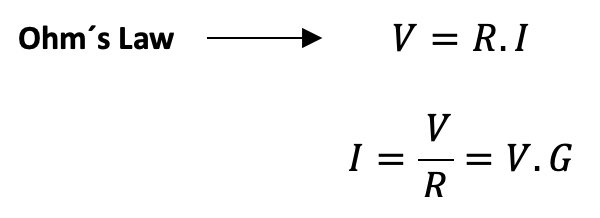
Give a look again at Figure 3B,  IK is represented by a green arrow and it is proportional to the voltage difference VM – EK and the resistance RK of the ionic channel. We replaced the resistance and used the conductance GK instead , and we get:

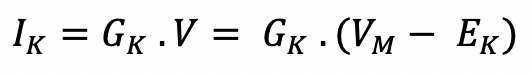
Until now we have just considered potassium channels to model the cell membrane. Can you imagine what will happen if we consider the rest of the ions involved in the action potential? Well, we will end up getting the Hodgkin–Huxley Equations! We will learn more about them in our next post. Keep safe and see you soon!

4. References

  1. Ermentrout, B., & Terman, D. H. (2010). The Hodgkin–Huxley Equations. In Mathematical foundations of neuroscience. New York: Springer.
  2. Nernst Equilibrium Potential – Resting Membrane Potential. Retrieved February 01, 2021, from https://www.physiologyweb.com/lecture_notes/resting_membrane_potential/resting_membrane_potential_nernst_equilibrium_potential.html